Albert Einstein allegedly called compound interest “the eighth wonder of the world,” and once you understand the math behind money, you’ll see why. A Compound Interest Calculator transforms abstract financial concepts into concrete numbers, showing exactly how your money multiplies over time, not through magic, but through mathematical precision.
Unlike simple interest, which calculates returns only on your original principal, compound interest calculates returns on both your principal and previously earned interest. This creates an exponential growth pattern that accelerates wealth building over time. The difference between someone who understands this principle and someone who doesn’t can mean hundreds of thousands of dollars over a lifetime.
The Compound Interest Calculator removes guesswork from financial planning. By inputting four essential variables, principal amount, interest rate, time period, and compounding frequency, you receive precise projections of future account values. This data-driven insight enables evidence-based investing decisions rather than emotional speculation.
Key Takeaways
- Compound interest grows exponentially by calculating returns on both principal and accumulated interest, creating accelerating wealth over time
- Compounding frequency matters significantly; daily compounding generates measurably higher returns than annual compounding on identical investments
- Time is the most powerful variable; doubling your investment timeline can more than double your final returns due to compounding acceleration
- Regular contributions amplify results dramatically; consistent deposits combined with compound interest create wealth-building momentum
- APY reveals true returns; Annual Percentage Yield accounts for compounding effects and provides an accurate comparison between financial products
What Is a Compound Interest Calculator and Why Does It Matter
A Compound Interest Calculator is a financial tool that projects future investment values by applying the compound interest formula to your specific inputs. It answers a fundamental question: “If I invest X dollars at Y percent interest for Z years, how much will I have?”
The calculator performs complex exponential calculations instantly, eliminating manual computation errors and providing visual representations of growth patterns. This transforms theoretical financial concepts into actionable data.
Compound Interest Formula
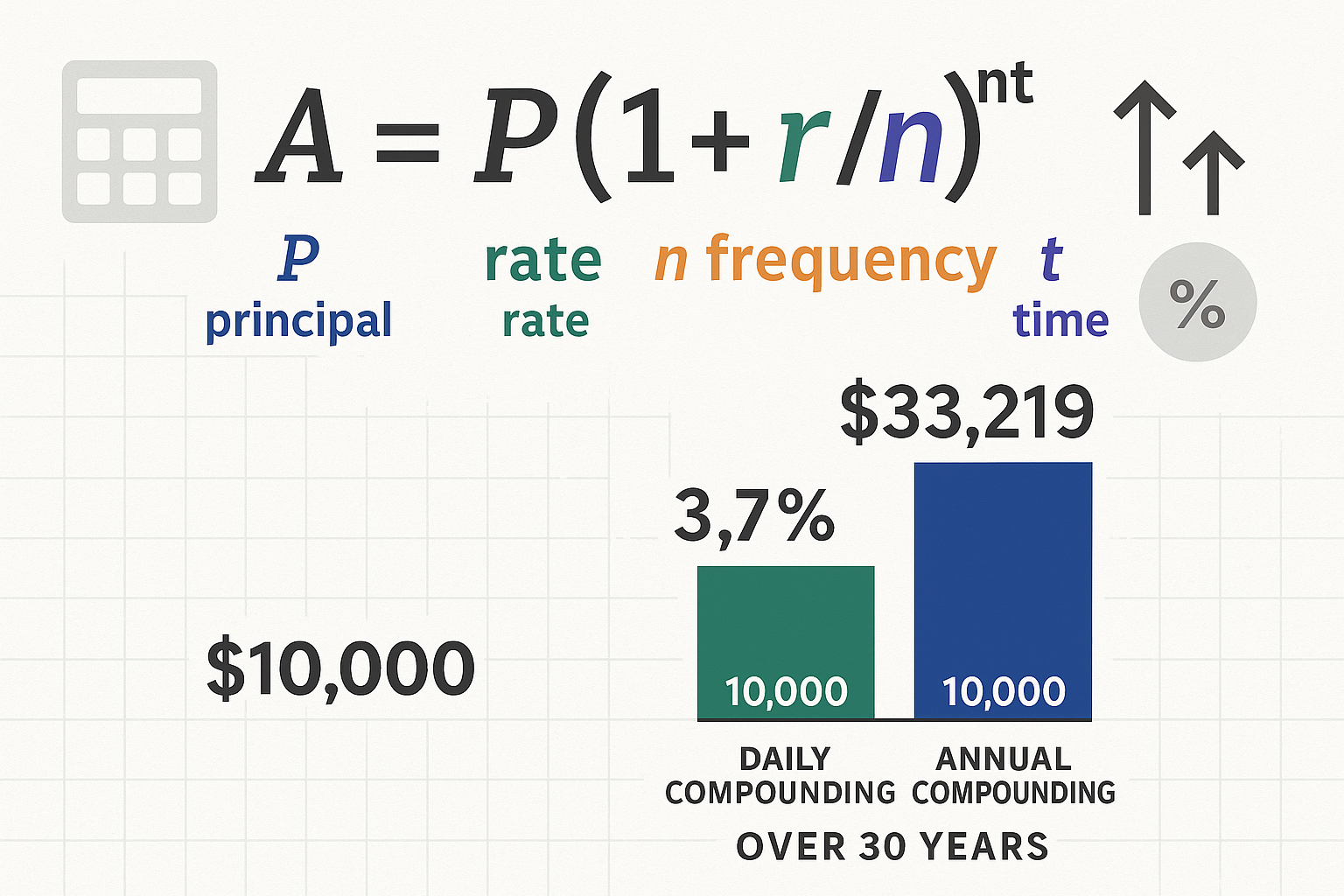
The compound interest formula is: A = P(1 + r/n)^(nt)
Where:
- A = Final maturity amount (future value)
- P = Principal (initial investment)
- r = Annual interest rate (expressed as a decimal)
- n = Compounding frequency per year
- t = Time in years
This formula captures the exponential nature of compound growth. Each compounding period, interest is calculated on an increasingly larger base amount, creating a snowball effect.
Example calculation: $10,000 invested at 8% annual interest for 30 years with annual compounding:
A = $10,000(1 + 0.08/1)^(1×30)
A = $10,000(1.08)^30
A = $10,000 × 10.0627
A = $100,627
The compound interest earned equals $90,627, more than nine times the original principal. This demonstrates the exponential power that makes compound interest the foundation of wealth building strategies.
Why Compound Interest Outperforms Simple Interest
Simple interest calculates returns only on the original principal. Using the same example with simple interest:
Simple Interest = P × r × t
Simple Interest = $10,000 × 0.08 × 30
Simple Interest = $24,000
The final amount would be $34,000 ($10,000 principal + $24,000 interest).
The difference? Compound interest produces $100,627 versus simple interest’s $34,000, a $66,627 advantage. This gap widens dramatically with longer timeframes and higher rates, illustrating why understanding compound versus simple interest is fundamental to financial literacy.
How to Use a Compound Interest Calculator Effectively
Effective calculator use requires understanding each input variable and how it influences outcomes. The four essential inputs work together to determine your financial trajectory.
The Four Critical Inputs
1. Principal Amount (P)
This represents your initial investment or current account balance. Whether you’re starting with $100 or $100,000, the calculator projects growth from this baseline.
The principal serves as the foundation. Larger initial investments produce proportionally larger returns, but even modest starting amounts grow substantially over extended periods through compounding.
2. Annual Interest Rate (r)
Enter the expected annual return as a percentage. For savings accounts, use the stated APY. For investment projections, consider historical market returns. The S&P 500 has averaged approximately 10% annually over the past century, though past performance doesn’t guarantee future results.
Conservative estimates produce more reliable projections. Overestimating returns creates unrealistic expectations and poor planning decisions.
3. Time Period (t)
Specify your investment timeline in years. This variable exerts exponential influence on outcomes; the longer the timeframe, the more dramatic the compounding effect.
A 40-year timeline doesn’t produce twice the returns of a 20-year timeline; it produces exponentially more due to compounding acceleration in later years. This principle underlies the importance of starting early with investing fundamentals.
4. Compounding Frequency (n)
Select how often interest compounds:
- Daily (n = 365): Most frequent, highest returns
- Monthly (n = 12): Common for savings accounts
- Quarterly (n = 4): Typical for some bonds
- Annually (n = 1): Simplest, lowest returns
More frequent compounding produces measurably better outcomes. An $1,000 investment at 8% for 40 years yields:
- Daily compounding: $24,518.56
- Annual compounding: $21,724.52
- Difference: $2,794.04
This $2,794 difference from compounding frequency alone demonstrates why understanding APY versus APR matters when comparing financial products.
Advanced Calculator Features
Sophisticated calculators include additional functionality:
Regular Contribution Modeling
Add monthly or annual deposits to see how consistent investing amplifies returns. Contributing $500 monthly to an account earning 7% annually produces dramatically different results than a one-time deposit.
Example: $10,000 initial investment with $500 monthly contributions at 7% for 30 years:
- Final balance: $733,367
- Total contributions: $190,000
- Interest earned: $543,367
The interest earned exceeds total contributions, a testament to compounding power combined with disciplined saving habits. This strategy aligns with systematic investing approaches.
Inflation Adjustment
Advanced calculators factor in inflation to show real purchasing power. A 3% inflation rate means money must grow faster than 3% annually just to maintain current buying power.
If your investment grows at 7% nominal but inflation runs at 3%, your real return is approximately 4%. This distinction between nominal and real returns prevents overestimating actual wealth accumulation.
Tax Optimization Comparisons
Some calculators model tax-deferred accounts (401(k), IRA) versus taxable accounts, showing how tax treatment affects net returns. Tax-deferred growth compounds faster because no annual taxes reduce the principal.
The Power of Compounding Frequency: Real Numbers
Compounding frequency significantly impacts outcomes, yet many investors overlook this variable. The mathematics reveal measurable differences.
Frequency Comparison Analysis
Consider $5,000 invested at 5% annual interest for 10 years across different compounding frequencies:
| Compounding Frequency | Formula Calculation | Final Amount | Interest Earned |
|---|---|---|---|
| Annually (n=1) | $5,000(1.05)^10 | $8,144.47 | $3,144.47 |
| Quarterly (n=4) | $5,000(1.0125)^40 | $8,218.10 | $3,218.10 |
| Monthly (n=12) | $5,000(1.004167)^120 | $8,235.05 | $3,235.05 |
| Daily (n=365) | $5,000(1.000137)^3650 | $8,243.32 | $3,243.32 |
Daily compounding produces $98.85 more than annual compounding, an 11.8% increase in interest earned from frequency alone. Over longer periods with larger principals, these differences become substantial.
Understanding Continuous Compounding
The theoretical limit of compounding frequency is continuous compounding, where n approaches infinity. The formula becomes:
A = Pe^(rt)
Where e ≈ 2.71828 (Euler’s number)
For our example: A = $5,000 × e^(0.05×10) = $8,243.61
Continuous compounding produces only $0.29 more than daily compounding, demonstrating that daily compounding approaches the mathematical maximum. This explains why financial institutions offering daily compounding provide near-optimal returns.
One-Year Growth Example
A $5,000 deposit earning 5% annual interest compounded monthly demonstrates a tangible short-term impact:
Monthly rate = 5% ÷ 12 = 0.4167%
A = $5,000(1.004167)^12
A = $5,255.81
Interest earned in one year: $255.81
With annual compounding, the same deposit would earn only $250.00, a $5.81 difference. While modest for one year, this pattern repeated over decades creates significant wealth gaps.
Time: The Most Powerful Variable in Compound Interest
Time exerts exponential influence on compound returns. Doubling your investment timeline doesn’t double returns; it multiplies them exponentially.
The Doubling Effect Illustrated
Compare $10,000 invested at 8% annual interest:
20-year timeline:
A = $10,000(1.08)^20 = $46,610
Interest earned: $36,610
40-year timeline:
A = $10,000(1.08)^40 = $217,245
Interest earned: $207,245
Doubling the time from 20 to 40 years increases returns from $36,610 to $207,245, a 466% increase in interest earned. This demonstrates compounding acceleration: returns grow faster in later years because the base amount is larger.
The Rule of 72
A quick estimation tool: Divide 72 by your annual interest rate to approximate how many years until your money doubles.
At 8% interest: 72 ÷ 8 = 9 years to double
At 6% interest: 72 ÷ 6 = 12 years to double
At 12% interest: 72 ÷ 12 = 6 years to double
This mental math helps evaluate whether investment timelines align with financial goals. Someone with 30 years until retirement at 8% returns can expect approximately 3.3 doublings, turning $50,000 into roughly $490,000 through compounding alone. See our full guide on The Rule of 72
Early Start Advantage
Two investors illustrate time’s critical importance:
Investor A: Contributes $5,000 annually from age 25 to 35 (10 years), then stops. Total contributions: $50,000.
Investor B: Contributes $5,000 annually from age 35 to 65 (30 years). Total contributions: $150,000.
Both earn 8% annually. At age 65:
- Investor A: $787,177 (despite stopping contributions at 35)
- Investor B: $566,416 (despite contributing 3× more)
Investor A’s 10-year head start produces $220,761 more wealth despite contributing $100,000 less. This counterintuitive result demonstrates why starting early matters more than contributing more; time amplifies compounding power exponentially.
This principle reinforces the value of building emergency funds and starting investments early, even with modest amounts.
Regular Contributions: Amplifying Compound Returns
Combining compound interest with regular contributions creates wealth-building momentum that far exceeds one-time investments.
The Contribution Multiplier Effect
Consider two scenarios over 15 years at 7% annual return:
Scenario 1: $10,000 one-time investment, no additional contributions
Final value: $27,590
Scenario 2: $10,000 initial investment + $6,000 annual contributions
Final value: $232,760
Regular contributions produce $205,170 additional wealth, an 844% increase over the one-time investment approach. The combination of consistent deposits and compound interest creates exponential acceleration.
Monthly Contribution Modeling
Monthly contributions smooth market volatility and maximize compounding opportunities. Instead of one annual $6,000 deposit, contributing $500 monthly allows each deposit to begin compounding immediately.
$500 monthly at 7% annual return for 30 years:
- Total contributions: $180,000
- Final value: $607,438
- Interest earned: $427,438
The interest earned ($427,438) exceeds total contributions ($180,000) by 237%. This demonstrates compound interest working alongside disciplined saving habits—a core principle of evidence-based investing.
Dollar-Cost Averaging Integration
Regular contributions naturally implement dollar-cost averaging, purchasing more shares when prices are low and fewer when prices are high. This systematic approach removes emotion from investing decisions and ensures consistent participation in market growth.
Combined with compound interest, dollar-cost averaging creates a powerful wealth-building system that benefits from both market appreciation and compounding returns.
Comparing Financial Products Using Compound Interest Calculators
Compound Interest Calculators enable objective comparison between savings accounts, certificates of deposit, bonds, and investment accounts by standardizing return projections.
APY: The True Comparison Metric
Annual Percentage Yield (APY) reflects actual annual returns after accounting for compounding effects. Unlike stated interest rates, APY enables apples-to-apples comparisons.
Example comparison:
Account A: 4.5% interest, compounded annually
APY = 4.5%
Account B: 4.4% interest, compounded daily
APY = 4.499%
Despite Account B’s lower stated rate, daily compounding produces nearly identical returns. The calculator reveals this equivalence that rates obscure.
When evaluating the best compound interest accounts, always prioritize APY over advertised interest rates.
Investment Account Projections
For equity investments, compound interest calculators model potential growth using historical average returns. While stocks don’t pay fixed interest, they produce average annual returns that compound similarly.
The S&P 500’s historical ~10% average annual return (including dividends) provides a reasonable projection baseline for diversified equity portfolios. Conservative investors might use 7-8% to account for volatility and lower-risk allocations.
30-year projection at different return rates ($10,000 initial + $500 monthly):
- 6% return: $505,365
- 8% return: $733,367
- 10% return: $1,056,580
The 4-percentage-point difference between 6% and 10% returns produces $551,215 additional wealth, demonstrating why investment selection and asset allocation strategies significantly impact long-term outcomes.
Tax-Advantaged Account Benefits
Tax-deferred accounts (401(k), Traditional IRA) allow full returns to compound without annual tax drag. Taxable accounts require paying taxes on dividends and capital gains, reducing the amount available for compounding.
Example: $10,000 growing at 8% for 30 years in a 24% tax bracket:
Tax-deferred account:
Full 8% compounds annually
Final value: $100,627
Taxable account (simplified):
Effective return ~6% after annual taxes
Final value: $57,435
The tax-deferred account produces $43,192 more wealth, a 75% advantage from tax treatment alone. This illustrates why maximizing contributions to tax-advantaged accounts should precede taxable investing for most individuals.
Understanding Calculator Output: Beyond the Final Number
Sophisticated calculators provide visual analysis tools that reveal growth patterns and inform strategic decisions.
Growth Charts and Visualization
Exponential growth curves show how compound interest accelerates over time. Early years display modest growth, while later years show dramatic increases as the compounding effect intensifies.
A typical 30-year growth chart reveals:
- Years 1-10: Gradual, linear-appearing growth
- Years 11-20: Noticeable acceleration
- Years 21-30: Dramatic exponential increase
This visual representation explains why patience matters in investing. The most significant wealth accumulation occurs in later years, rewarding those who maintain consistent strategies through market cycles.
Pie Chart Analysis
Pie charts display the proportion of the final value from principal contributions versus interest earned. This visualization highlights compound interest’s contribution to total wealth.
Example breakdown after 25 years:
- Principal contributions: 35%
- Interest earned: 65%
Interest comprises nearly two-thirds of final wealth, demonstrating that compound returns, not just saving, drive wealth accumulation. This insight reinforces the importance of optimizing return rates and investment selection.
Year-by-Year Summary Tables
Detailed tables show annual progression:
| Year | Beginning Balance | Contribution | Interest Earned | Ending Balance |
|---|---|---|---|---|
| 1 | $10,000 | $6,000 | $1,120 | $17,120 |
| 2 | $17,120 | $6,000 | $1,618 | $24,738 |
| 3 | $24,738 | $6,000 | $2,152 | $32,890 |
These tables reveal compounding acceleration, and interest earned increases each year even with identical contributions. Year 1 produces $1,120 interest; Year 3 produces $2,152—a 92% increase despite constant contribution amounts.
This granular view helps identify optimal contribution strategies and withdrawal timing for retirement planning using principles like the 4% rule.
Real-World Applications: Putting the Calculator to Work
Compound Interest Calculators solve practical financial planning challenges across multiple scenarios.
Retirement Planning
Determine required monthly contributions to reach retirement goals:
Goal: $1,500,000 in 30 years
Current savings: $50,000
Expected return: 8% annually
Required monthly contribution: $1,435
The calculator reverse-engineers contribution requirements from desired outcomes, transforming abstract retirement goals into concrete monthly action items.
Alternatively, project current savings trajectories to assess whether existing strategies will meet goals or require adjustment.
Education Funding
Calculate 529 plan growth to fund college expenses:
Current 529 balance: $20,000
Monthly contribution: $300
Timeline: 15 years
Expected return: 6%
Projected value: $125,650
This projection informs whether current contributions will cover anticipated education costs or require increases. The calculator provides data-driven answers rather than hopeful guesses.
Emergency Fund Growth
Model how emergency fund savings grow in high-yield savings accounts:
Initial deposit: $5,000
Monthly addition: $400
Account APY: 4.5%
Timeline: 2 years
Final value: $15,239
While emergency funds prioritize liquidity over returns, compound interest still contributes meaningful growth. The calculator shows how consistent saving combined with a competitive APY builds financial security.
Debt Payoff Comparison
Use compound interest logic in reverse to compare debt payoff strategies. Credit card debt compounds against you; the same exponential mathematics that builds wealth also accelerates debt.
Example: $10,000 credit card balance at 18% APR
Minimum payments extend the payoff to 15+ years and cost $12,000+ in interest
The calculator demonstrates why aggressive debt elimination should precede aggressive investing for most individuals. Eliminating 18% interest debt provides guaranteed 18% “returns.”
Common Mistakes When Using Compound Interest Calculators
Even powerful tools produce misleading results when used incorrectly. Avoid these frequent errors:
Overestimating Return Rates
Using unrealistic return assumptions (12%+ for conservative portfolios) creates false confidence and inadequate saving rates. Historical market returns don’t guarantee future performance, and individual portfolio returns vary based on allocation and timing.
Solution: Use conservative estimates. For diversified equity portfolios, 7-8% provides reasonable long-term projections. For bonds and savings accounts, use stated APY.
Ignoring Inflation
Nominal returns don’t reflect purchasing power. A 7% return with 3% inflation produces 4% real growth. Failing to account for inflation overestimates actual wealth accumulation.
Solution: Subtract expected inflation (2-3% historically) from return rates, or use calculators with built-in inflation adjustment to see real purchasing power projections.
Neglecting Taxes
Tax-deferred and taxable account returns differ significantly. Using pre-tax return rates for taxable accounts overstates actual growth.
Solution: Reduce expected returns by your marginal tax rate for taxable accounts, or use calculators that model tax impacts explicitly.
Assuming Constant Returns
Markets fluctuate. Using 8% average returns doesn’t mean earning exactly 8% every year—actual returns vary from -30% to +30% in different years. Calculators using constant returns don’t capture volatility impact.
Solution: Understand calculator projections represent averages. Actual outcomes will vary based on market performance sequence, particularly near retirement when sequence-of-returns risk intensifies.
Forgetting Fees
Investment fees compound negatively. A 1% annual fee doesn’t reduce returns by 1%; it reduces them by 1% compounded annually, creating a substantial long-term impact.
Example: $100,000 growing at 8% for 30 years:
- 0% fees: $1,006,266
- 1% fees (7% net return): $761,226
- Difference: $245,040
That 1% fee costs $245,040 over 30 years—nearly 25% of potential wealth. When projecting investment growth, subtract expense ratios from expected returns for accurate modeling.
Advanced Calculator Features for Sophisticated Planning
Beyond basic projections, advanced calculators offer specialized functionality for complex scenarios.
Variable Contribution Modeling
Model contribution increases over time to reflect salary growth:
Years 1-5: $500 monthly
Years 6-10: $750 monthly
Years 11-30: $1,000 monthly
This creates more realistic projections than constant contribution assumptions, particularly for early-career professionals expecting income growth.
Multiple Account Aggregation
Combine projections across multiple accounts (401(k), IRA, taxable brokerage, savings) to see total net worth trajectory. This holistic view reveals whether diversified savings strategies collectively meet goals.
Withdrawal Modeling
Project account longevity with regular withdrawals during retirement. Input expected withdrawal amounts and see how long assets last under different return scenarios.
This functionality helps validate retirement readiness and stress-test plans against market volatility using sustainable withdrawal strategies.
Monte Carlo Simulation
Sophisticated calculators run thousands of scenarios with variable returns to show probability distributions of outcomes. Instead of single projections, you see:
- 90% probability of achieving at least $800,000
- 50% probability of achieving $1,200,000
- 10% probability of achieving $1,800,000+
This probabilistic approach provides more realistic planning frameworks than single-point estimates.
The Behavioral Psychology of Compound Interest
Understanding compound interest intellectually differs from internalizing it behaviorally. Calculators bridge this gap by making abstract concepts tangible.
Visualization Creates Motivation
Seeing concrete projections—”$500 monthly becomes $607,438 in 30 years”- transforms vague financial advice into compelling motivation. The calculator quantifies the opportunity cost of delaying contributions or choosing lower-return accounts.
This visualization combats present bias (valuing immediate consumption over future wealth) by making future outcomes feel real and achievable.
Small Changes, Large Impacts
Calculators reveal how minor adjustments produce significant outcomes:
Scenario A: $400 monthly for 30 years at 7% = $486,991
Scenario B: $500 monthly for 30 years at 7% = $607,438
Difference from $100 extra monthly: $120,447
That additional $100 monthly ($36,000 total over 30 years) produces $120,447 extra wealth—a 335% return on the incremental contribution through compounding. This insight motivates budget optimization and spending prioritization.
Patience Becomes Strategy
Compound interest rewards patience disproportionately. Calculators demonstrate that the final 10 years of a 30-year plan produce more wealth than the first 20 years combined—a powerful argument against panic selling during market downturns.
Understanding this mathematical reality helps investors maintain discipline through market emotion cycles and avoid behavior that undermines long-term compounding.
Building Your Compound Interest Strategy
Effective wealth building requires translating calculator insights into actionable strategies.
Step 1: Establish Clear Goals
Define specific targets: “Accumulate $1,000,000 for retirement by age 65” or “Save $100,000 for a home down payment in 7 years.” Specific goals enable precise calculator modeling.
Step 2: Assess Current Position
Input existing savings, current contribution rates, and realistic return expectations based on current allocation. This baseline projection shows whether the current trajectory meets goals.
Step 3: Identify Gaps
Compare current trajectory to goals. If projections fall short, the calculator reveals required adjustments:
- Increase monthly contributions
- Extend timeline
- Optimize returns through better account selection
- Reduce fees through low-cost index funds
Step 4: Optimize Compounding Variables
Maximize compound interest efficiency:
Increase contribution frequency: Monthly contributions compound faster than annual lump sums
Maximize compounding frequency: Choose daily over annual compounding when available
Minimize fees: Every 0.1% fee reduction compounds positively over decades
Extend timeline: Start earlier to maximize time’s exponential impact
Optimize tax treatment: Prioritize tax-advantaged accounts for maximum compounding
Step 5: Monitor and Adjust
Revisit calculator projections annually. Update inputs based on:
- Actual returns versus projections
- Contribution changes
- Goal modifications
- Timeline adjustments
Regular monitoring ensures strategies remain aligned with evolving circumstances and market conditions.
The Compound Interest Calculator as a Financial Literacy Tool
Beyond personal planning, compound interest calculators serve as educational instruments that build fundamental financial literacy.
Teaching Exponential Thinking
Most people think linearly, doubling inputs doubles outputs. Compound interest requires exponential thinking, where small input changes produce disproportionate output changes.
Calculators make exponential mathematics accessible without requiring advanced math skills. This democratizes financial understanding and empowers informed decision-making.
Quantifying Opportunity Cost
Every financial decision involves opportunity cost, what you sacrifice by choosing one option over another. Compound interest calculators quantify these trade-offs:
Buying a $30,000 car versus a $20,000 car:
The $10,000 difference invested at 8% for 30 years grows to $100,627. The “real cost” of the luxury car isn’t $10,000, it’s $100,627 in forgone compound growth.
This perspective doesn’t prohibit spending, but it informs spending by revealing true long-term costs. Similar logic applies to car buying decisions and rent versus buy calculations.
Demonstrating Time Value of Money
A dollar today is worth more than a dollar tomorrow because today’s dollar can compound. Calculators make this abstract principle concrete:
$1,000 today at 7% becomes $1,967 in 10 years
$1,000 received in 10 years remains $1,000
The time value difference is $967, a 96.7% premium for immediate access. This concept underlies all financial valuation, from bond pricing to discounted cash flow analysis.
💰 Compound Interest Calculator
Conclusion: Turning Knowledge Into Wealth
The Compound Interest Calculator transforms abstract financial principles into actionable wealth-building strategies. Understanding the math behind money, how principal, rate, time, and frequency interact exponentially, provides the foundation for evidence-based investing decisions.
Key insights to implement immediately:
Start now, not later. Time exerts exponential influence on compound returns. A 10-year head start produces more wealth than tripling contributions later. Even modest amounts grow substantially over extended periods through compounding.
Maximize compounding efficiency. Choose accounts with daily compounding over annual, minimize fees that compound negatively, and prioritize tax-advantaged accounts that allow full returns to compound without annual tax drag.
Combine discipline with mathematics. Regular contributions amplified by compound interest create wealth-building momentum that far exceeds sporadic investing. Systematic approaches remove emotion and ensure consistent participation in compound growth.
Use calculators for planning, not prediction. Projections represent averages based on assumptions. Actual outcomes vary with market performance, but calculators provide essential frameworks for setting goals, measuring progress, and adjusting strategies.
Understand opportunity costs. Every financial decision involves trade-offs. Compound interest calculators quantify what you sacrifice by choosing one option over another, enabling informed decisions based on data rather than impulse.
The difference between financial success and struggle often reduces to understanding and applying compound interest principles. Those who harness exponential mathematics build wealth systematically; those who ignore it struggle perpetually.
Next steps:
- Use a compound interest calculator to project your current savings trajectory
- Identify gaps between current projections and financial goals
- Adjust variables (contributions, timeline, account selection) to close gaps
- Implement changes immediately; every month delayed costs compound growth
- Monitor progress annually and adjust strategies based on actual performance
Compound interest doesn’t require exceptional intelligence or luck; it requires understanding, discipline, and time. The calculator provides understanding. Your actions provide discipline. Starting today provides time.
The math behind money is precise, logical, and accessible. Use it to your advantage.
References
[1] Board of Governors of the Federal Reserve System. “Consumer Credit – G.19.” Federal Reserve Statistical Release, 2025.
[2] Morningstar Investment Research. “Annual Returns and Compounding Effects in Equity Markets.” Morningstar Direct Database, 2025.
[3] U.S. Securities and Exchange Commission. “Compound Interest Calculator.” Investor.gov, Office of Investor Education and Advocacy, 2025.
[4] CFA Institute. “Time Value of Money: Foundations of Financial Analysis.” CFA Program Curriculum, Level I, 2025.
[5] Bureau of Labor Statistics. “Consumer Price Index and Inflation Data.” U.S. Department of Labor, 2025.
[6] Internal Revenue Service. “Tax-Advantaged Retirement Accounts: Publication 590-A.” Department of the Treasury, 2025.
Author Bio
Max Fonji is a data-driven financial educator and the voice behind The Rich Guy Math. With expertise in valuation principles, risk management, and evidence-based investing, Max translates complex financial concepts into clear, actionable insights. His analytical approach combines mathematical precision with practical application, helping readers understand the cause-and-effect relationships that drive wealth building. Max’s work focuses on teaching financial literacy through numbers, logic, and proven frameworks rather than speculation or hype.
Educational Disclaimer
This article provides educational information about compound interest calculations and wealth-building principles. It does not constitute financial advice, investment recommendations, or personalized planning guidance. Individual financial situations vary based on risk tolerance, time horizon, tax circumstances, and specific goals. Compound interest projections represent mathematical calculations based on stated assumptions; actual investment returns fluctuate and may differ significantly from projections. Past market performance does not guarantee future results. Consult qualified financial professionals before making investment decisions. The author and The Rich Guy Math assume no liability for financial outcomes resulting from information presented in this article.
Frequently Asked Questions About Compound Interest Calculators
What is the compound interest formula and how does it work?
The compound interest formula is A = P(1 + r/n)^(nt), where A equals the final amount, P is the principal, r is the annual interest rate as a decimal, n is the compounding frequency per year, and t is time in years. This formula calculates returns on both principal and accumulated interest, creating exponential growth that accelerates over time.
How does compounding frequency affect my returns?
Compounding frequency significantly impacts final returns. Daily compounding produces higher returns than monthly, quarterly, or annual compounding on identical investments. For example, $10,000 at 8% for 40 years yields $24,518.56 with daily compounding versus $21,724.52 with annual compounding—a $2,794.04 difference from frequency alone.
What’s the difference between APY and interest rate?
APY (Annual Percentage Yield) reflects actual annual returns after accounting for compounding effects, while the stated interest rate doesn’t include compounding impact. APY provides accurate comparisons between financial products with different compounding frequencies. Always prioritize APY over advertised rates when evaluating accounts.
How do regular contributions amplify compound interest?
Regular contributions create wealth-building momentum by continuously adding principal that begins compounding immediately. A $10,000 initial investment with $500 monthly contributions at 7% for 30 years grows to $607,438, compared to just $76,123 without contributions—an 8× increase from consistent deposits combined with compound interest.
Should I pay off debt or invest for compound interest?
Generally, eliminate high-interest debt before aggressive investing. Credit card debt at 18% APR compounds against you faster than most investments compound for you. Paying off 18% debt provides guaranteed 18% “returns.” Prioritize debt elimination, then redirect those payments toward investments that compound positively.
How does inflation affect compound interest calculations?
Inflation reduces purchasing power of future dollars. A 7% nominal return with 3% inflation produces approximately 4% real return. Subtract expected inflation from return rates or use calculators with inflation adjustment to see real wealth accumulation rather than nominal dollar growth.
What return rate should I use for stock market projections?
The S&P 500 has averaged approximately 10% annually over the past century, but conservative projections use 7–8% to account for volatility and diversification. Individual portfolio returns vary based on allocation, fees, and timing. Use conservative estimates to avoid overestimating future wealth and undersaving.
How do investment fees impact compound returns?
Fees compound negatively over time. A 1% annual fee on $100,000 growing at 8% for 30 years costs $245,040 in forgone returns—nearly 25% of potential wealth. Minimize fees through low-cost index funds and subtract expense ratios from expected returns when projecting growth.







