Imagine you’re offered a choice: receive $10,000 today or $10,000 five years from now. If you’re like most people, you’d grab the money today without hesitation. But why? Beyond the obvious appeal of instant gratification, there’s a powerful financial principle at work here—one that separates savvy investors from those who leave money on the table. Present Value is the mathematical backbone of nearly every smart financial decision you’ll ever make, from evaluating investment opportunities to understanding how dividend stocks create wealth over time.
Whether you’re comparing job offers with different bonus structures, deciding whether to take a lump sum or annuity payment, or evaluating stocks and bonds, understanding Present Value gives you a superpower: the ability to compare money across different time periods on an apples-to-apples basis. In simple terms, Present Value means determining what future money is worth in today’s dollars.
This guide will walk you through everything you need to know about Present Value, from the basic formula to real-world examples that’ll make you see your financial decisions in a whole new light.
TL;DR Summary
- Present Value (PV) is the current worth of a future sum of money or stream of cash flows, discounted at a specific rate of return
- The PV formula is: PV = FV / (1 + r)^n, where FV is the future value, r is the discount rate, and n is the number of periods
- Money today is worth more than the same amount in the future due to inflation, opportunity cost, and earning potential
- PV is essential for comparing investment opportunities, valuing bonds and stocks, and making informed financial decisions
- Higher discount rates result in lower present values, reflecting greater risk or better alternative investment opportunities
What Is Present Value?
Present Value (PV) represents the current value of a future amount of money or a series of cash flows, given a specified rate of return. Think of it as financial time travel, you’re bringing future dollars back to today to see what they’re really worth.
The concept exists because of a fundamental truth in finance: a dollar today is worth more than a dollar tomorrow. This isn’t just about inflation eating away at purchasing power (though that’s part of it). It’s about opportunity cost—what you could do with that money if you had it now instead of later. Investopedia – Present Value
Here’s a real-world story that illustrates this perfectly: In 2015, a lottery winner faced a choice between $310 million paid over 30 years or a $193 million lump sum. Most financial advisors recommended the lump sum, even though it seemed like $117 million less. Why? Because the Present Value of that $193 million today, invested wisely, could potentially grow to far more than $310 million over 30 years. The lottery commission was essentially using Present Value calculations to determine that lump sum amount; they knew what those future payments were worth in today’s dollars.
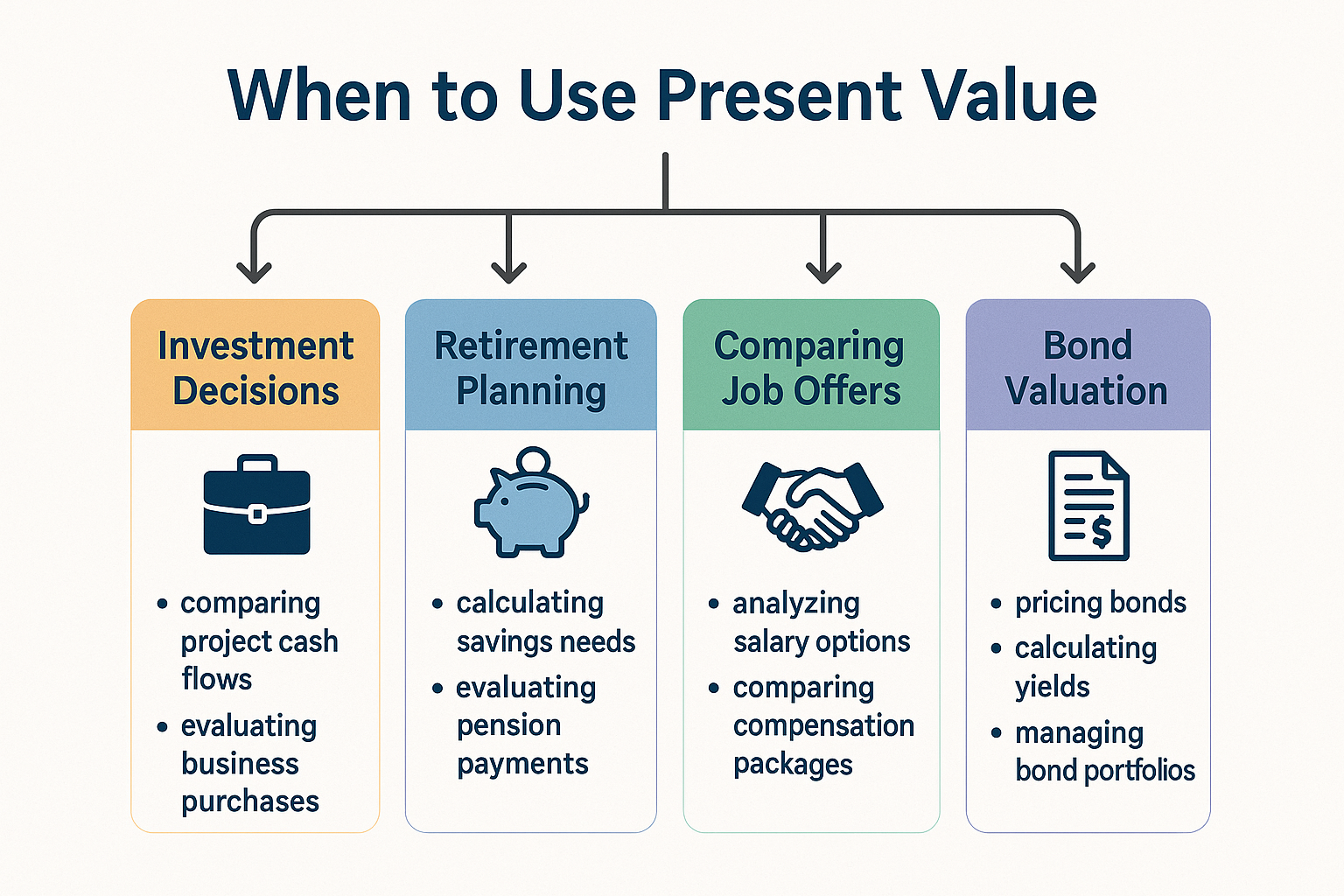
Why Present Value Matters in Your Financial Life
Understanding PV helps you:
- Compare investment opportunities with different payout structures
- Evaluate whether to take lump sums or payment plans for settlements, pensions, or lottery winnings
- Determine the fair price for bonds, stocks, and real estate
- Make better borrowing decisions by understanding the true cost of loans
- Plan for retirement by calculating how much you need to save today
- Understand how the stock market creates wealth through compounding returns
When you grasp Present Value, you start seeing through marketing gimmicks like “No payments for 12 months!” and understand the smart moves that actually build wealth.
The Present Value Formula: Breaking Down the Math

The basic Present Value formula might look intimidating at first, but it’s actually quite logical once you understand each component:
PV = FV / (1 + r)^n
Where:
- PV = Present Value (what we’re solving for)
- FV = Future Value (the amount of money in the future)
- r = Discount rate (expressed as a decimal)
- n = Number of time periods
Let’s break down what each piece means:
Future Value (FV)
This is the amount of money you’ll receive in the future. It could be a single payment (like a bond maturity) or the final value of a series of payments.
Discount Rate (r)
This is the rate of return you could earn on alternative investments with similar risk, or the interest rate that reflects the time value of money. The discount rate is crucial because it reflects both the opportunity cost of capital and the risk involved. SEC – Investor Education
A higher discount rate means:
- Greater uncertainty or risk
- Better alternative investment opportunities are available
- Lower present value for the same future amount
Number of Periods (n)
This represents how many time periods (years, months, quarters) until you receive the money. The further into the future, the less money is worth today.
The Power of Exponents
Notice that (1 + r)^n part? That exponent is critical. It means the effect compounds over time. Money 10 years away isn’t just worth 10% less per year; it compounds, making distant money worth dramatically less in present value terms.
Present Value Formula Examples: From Simple to Complex
Let’s work through several examples that progress from basic to more advanced scenarios. Grab a calculator (or use the interactive tool below) and follow along!
Example 1: Simple Single Payment
Scenario: Your friend promises to pay you $5,000 in 3 years. If you could invest money today at 6% annual return, what’s the present value of that promise?
Given:
- FV = $5,000
- r = 0.06 (6%)
- n = 3 years
Calculation:
PV = $5,000 / (1 + 0.06)^3
PV = $5,000 / (1.06)^3
PV = $5,000 / 1.191016
PV = $4,198.10Interpretation: That $5,000 payment three years from now is worth only $4,198.10 today. In other words, if someone offered you $4,200 cash today instead of $5,000 in three years, you’d be slightly better off taking the cash.
Example 2: The Impact of Different Discount Rates
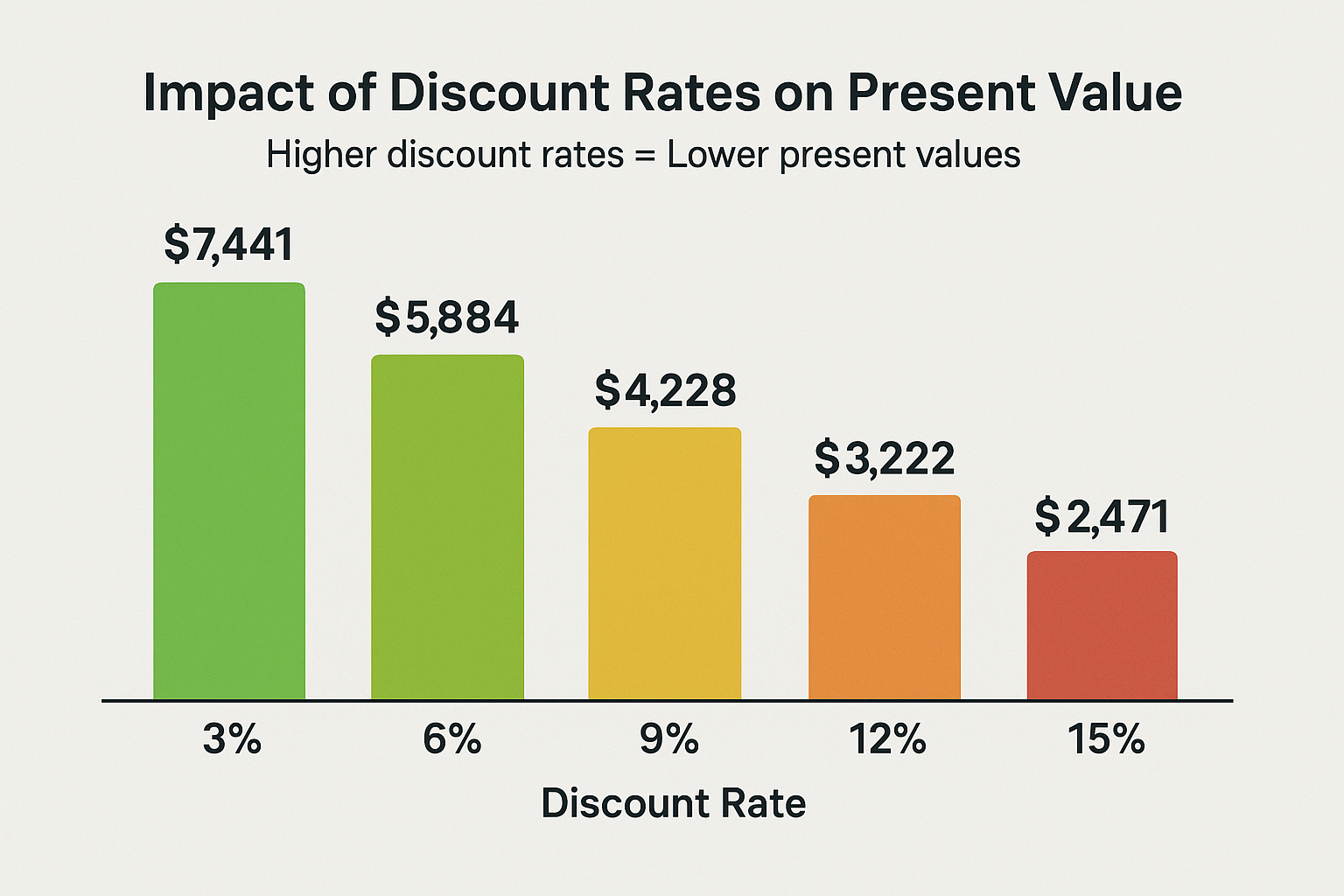
Let’s see how changing the discount rate affects the present value of that same $5,000 payment in 3 years:
| Discount Rate | Present Value | Difference from 6% |
|---|---|---|
| 3% | $4,576.54 | +$378.44 |
| 6% | $4,198.10 | baseline |
| 9% | $3,860.92 | -$337.18 |
| 12% | $3,558.90 | -$639.20 |
Key insight: As the discount rate increases, the present value decreases significantly. This makes intuitive sense—if you have better investment opportunities (a higher discount rate), future money becomes less attractive relative to money today. Federal Reserve – Discount Rates
Example 3: Long-Term vs. Short-Term Money
What’s worth more: $10,000 in 5 years or $10,000 in 20 years? Let’s assume a 7% discount rate:
5-year payment:
PV = $10,000 / (1.07)^5
PV = $10,000 / 1.402552
PV = $7,129.8620-year payment:
PV = $10,000 / (1.07)^20
PV = $10,000 / 3.869684
PV = $2,584.19Wow! The same $10,000 amount is worth nearly 3 times more if you receive it in 5 years versus 20 years. This demonstrates why understanding market cycles and long-term investing requires patience—but also why getting returns sooner matters.
Example 4: Real Estate Investment Decision
Scenario: You’re considering buying a rental property. A real estate investor offers to buy it from you in 10 years for $500,000. You want at least a 10% annual return on your real estate investments. What’s the maximum you should pay today?
Given:
- FV = $500,000
- r = 0.10 (10%)
- n = 10 years
Calculation:
PV = $500,000 / (1.10)^10
PV = $500,000 / 2.593742
PV = $192,772.47Decision: You shouldn’t pay more than approximately $192,772 for this property if you want a 10% return. If the seller wants $250,000, you’d need to negotiate down or look for a different investment opportunity.
Present Value of an Annuity: When Payments Come in Streams
So far, we’ve looked at single future payments. But what about situations where you receive multiple payments over time—like rental income, bond coupon payments, or dividend income from stocks? That’s where the Present Value of an Annuity comes in.
The Annuity Formula
For a series of equal payments received at regular intervals:
PV = PMT × [(1 – (1 + r)^-n) / r]
Where:
- PMT = Payment amount per period
- r = Discount rate per period
- n = Number of periods
Example 5: Valuing a Pension Offer
Scenario: You’re retiring and your company offers you $3,000 per month for the next 20 years, or a lump sum of $450,000 today. Assuming you could safely invest money at 5% annually, which should you take?
First, we need to convert to annual figures:
- Annual payment: $3,000 × 12 = $36,000
- Annual rate: 5% = 0.05
- Periods: 20 years
Calculation:
PV = $36,000 × [(1 - (1.05)^-20) / 0.05]
PV = $36,000 × [(1 - 0.376889) / 0.05]
PV = $36,000 × [0.623111 / 0.05]
PV = $36,000 × 12.46221
PV = $448,640Decision: The present value of the payment stream ($448,640) is slightly less than the lump sum offer ($450,000). The lump sum is the better deal—but just barely! This is why understanding these calculations matters; you could easily make the wrong choice without them.
Present Value in Stock Market Investing
Understanding Present Value isn’t just theoretical—it’s fundamental to how investors value stocks and make decisions about why the stock market goes up over time.
Dividend Discount Model (DDM)
One of the most common applications of PV in stock investing is the Dividend Discount Model, which values a stock based on the present value of all its future dividend payments.
For a stock paying constant dividends forever (a perpetuity):
Stock Value = Annual Dividend / Discount Rate
Example 6: A stable utility company pays $2.50 annual dividend per share. If you require a 7% return, what’s a fair price for the stock?
Stock Value = $2.50 / 0.07
Stock Value = $35.71If the stock is trading at $30, it might be undervalued. If it’s at $40, it might be overvalued based on this simple model.
Why Some Investors Lose Money
Many investors lose money because they don’t understand present value concepts. They chase stocks based on hype rather than calculating what future cash flows are actually worth today. Understanding why people lose money in the stock market often comes down to ignoring fundamental valuation principles like PV.
Advantages and Limitations of Present Value Analysis
Advantages of Using Present Value
1. Objective Comparison Across Time
PV provides an apples-to-apples comparison of money received at different times, removing the guesswork from financial decisions.
2. Accounts for Opportunity Cost
By using a discount rate, PV explicitly considers what else you could do with your money—a critical factor many people overlook.
3. Incorporates Risk
Higher-risk investments should use higher discount rates, automatically reducing their present value and requiring higher future returns to justify the investment.
4. Universal Application
From personal finance decisions to corporate capital budgeting, PV works across all financial contexts.
5. Reveals True Value
Marketing claims like “Save $10,000 over 5 years!” can be evaluated properly when you calculate the present value of those savings.
Limitations and Challenges
1. Discount Rate Uncertainty
Choosing the “right” discount rate is part art, part science. Small changes in the rate can dramatically affect present value calculations.
2. Assumes Constant Rates
Most PV formulas assume discount rates stay constant, but real-world interest rates and investment returns fluctuate.
3. Doesn’t Account for All Factors
PV focuses on financial returns but ignores qualitative factors like job satisfaction, lifestyle preferences, or personal circumstances.
4. Future Cash Flow Uncertainty
You’re making assumptions about future payments that may not materialize as expected—especially relevant for startup investments or speculative stocks.
5. Complexity with Irregular Payments
When payments vary in amount or timing, calculations become more complex and require spreadsheet tools or financial calculators.
Present Value vs Future Value: Understanding the Relationship
Present Value and Future Value are two sides of the same coin—they’re mathematically inverse concepts:
| Aspect | Present Value (PV) | Future Value (FV) |
|---|---|---|
| Definition | Current worth of future money | What current money will be worth later |
| Direction | Discounting (going backward in time) | Compounding (going forward in time) |
| Formula | PV = FV / (1 + r)^n | FV = PV × (1 + r)^n |
| Use Case | “What should I pay today?” | “How much will I have later?” |
| Application | Valuing investments, bonds, offers | Retirement planning, savings goals |
Example 7: Let’s see both concepts in action:
You invest $5,000 today at 8% annual return for 10 years.
Future Value calculation:
FV = $5,000 × (1.08)^10
FV = $5,000 × 2.158925
FV = $10,794.62Now, working backward with Present Value:
PV = $10,794.62 / (1.08)^10
PV = $10,794.62 / 2.158925
PV = $5,000They’re perfectly inverse! This relationship is why understanding one helps you understand the other.
How to Interpret and Use Present Value in Investment Decisions
Step-by-Step Decision Framework
Step 1: Identify All Cash Flows
List every payment you’ll receive or make, and when each occurs.
Step 2: Determine the Appropriate Discount Rate
Consider:
- Current interest rates on safe investments (Treasury bonds)
- Risk level of the investment
- Your personal required rate of return
- Alternative investment opportunities
Step 3: Calculate Present Value
Use the formulas we’ve covered or the interactive calculator below.
Step 4: Compare to Cost or Alternatives
- If PV > Cost, the investment may be worthwhile
- If PV < Cost, look for better opportunities
- Compare the PVs of different investment options
Step 5: Consider Qualitative Factors
Numbers aren’t everything—also weigh personal circumstances, risk tolerance, and goals.
Real-World Application: Evaluating a Side Business
Scenario: You’re considering buying a small online business for $50,000. The seller provides financial records showing it generates $12,000 annual profit. You want a 15% return to compensate for the risk and effort involved.
If we assume the business will run for 10 years and then be worth nothing:
PV = $12,000 × [(1 - (1.15)^-10) / 0.15]
PV = $12,000 × 5.0188
PV = $60,225.60Decision: The present value ($60,225.60) exceeds the asking price ($50,000) by about $10,000. This suggests it could be a good investment at this price, assuming the profit projections are accurate.
However, you should also consider:
- Can you verify those profit numbers?
- How stable is the revenue?
- What’s your exit strategy after 10 years?
- What’s your time commitment?
This is where PV analysis combines with due diligence to make smart financial moves.
Common Mistakes to Avoid When Using Present Value
1: Using the Wrong Discount Rate
The Problem: Applying a 3% discount rate to a high-risk startup investment, or using 15% for government bonds.
The Fix: Match your discount rate to the investment’s risk profile. Higher risk = higher discount rate.
2: Ignoring Inflation
The Problem: Using nominal rates when you should use real (inflation-adjusted) rates, or vice versa.
The Fix: Be consistent—use nominal cash flows with nominal discount rates, or real cash flows with real discount rates.
3: Forgetting About Taxes
The Problem: Calculating PV on pre-tax cash flows when you’ll actually receive after-tax amounts.
The Fix: Adjust cash flows for expected taxes to get a realistic present value.
4: Over-Precision with Uncertain Inputs
The Problem: Calculating PV to the penny when your discount rate and cash flow estimates are rough guesses.
The Fix: Recognize that PV is a tool for comparison and decision-making, not absolute precision. Round to reasonable figures.
5: Ignoring the Timing of Payments
The Problem: Assuming all annual payments come at year-end when they actually arrive monthly or quarterly.
The Fix: Adjust your formula for the actual payment timing, or use monthly/quarterly periods with corresponding discount rates.
Present Value in Different Financial Contexts
Bond Valuation
Bonds are essentially PV problems in disguise. A bond’s fair price equals the present value of all future coupon payments plus the present value of the principal repayment.
Example 8: A 5-year bond pays $50 annual coupons and returns $1,000 at maturity. If current market rates are 6%, what’s it worth?
PV of coupons: $50 × 4.2124 = $210.62
PV of principal: $1,000 / (1.06)^5 = $747.26
Total Bond Value: $957.88
This is why bond prices fall when interest rates rise—the discount rate increases, lowering the present value of future payments.
Retirement Planning
Present Value helps answer: “How much do I need to save today to retire comfortably?”
If you want $50,000 annual income for 30 years in retirement, and you can earn 6% on your investments:
PV = $50,000 × [(1 - (1.06)^-30) / 0.06]
PV = $50,000 × 13.7648
PV = $688,240You’d need approximately $688,240 saved at retirement to generate that income stream. This is crucial for making your kids millionaires through early investing—starting early dramatically reduces the required present value.
Lease vs. Buy Decisions
Should you lease that car for $400/month for 3 years, or buy it for $35,000?
PV of lease payments (at 5% annual rate, converted to monthly):
Monthly rate: 0.05/12 = 0.004167
Periods: 36 months
PV = $400 × [(1 - (1.004167)^-36) / 0.004167]
PV = $400 × 33.9703
PV = $13,588The present value of leasing ($13,588) is significantly less than buying ($35,000), but remember—you don’t own the car at the end. You’d need to factor in the car’s residual value after 3 years to make a fair comparison.
Advanced Present Value Concepts
Net Present Value (NPV)
Net Present Value takes PV one step further by subtracting the initial investment cost:
NPV = PV of future cash flows – Initial investment
- NPV > 0: Investment adds value; generally accepted
- NPV = 0: Investment breaks even; neutral
- NPV < 0: Investment destroys value; generally reject
This is the gold standard for corporate capital budgeting decisions.
Discount Rate Selection: WACC and CAPM
Large companies use sophisticated methods to determine discount rates:
WACC (Weighted Average Cost of Capital): Blends the cost of debt and equity financing based on the company’s capital structure.
CAPM (Capital Asset Pricing Model): Calculates required return based on systematic risk:
Required Return = Risk-Free Rate + Beta × (Market Return - Risk-Free Rate)For personal finance, simpler approaches work fine:
- Low risk: Use current Treasury bond rates (4-5% in 2025)
- Medium risk: Use average stock market returns (7-10%)
- High risk: Use 12-15%+ depending on uncertainty
Perpetuities and Growing Perpetuities
A perpetuity is a payment that continues forever. Its present value is simply:
PV = Payment / Discount Rate
A growing perpetuity increases at a constant rate:
PV = Payment / (Discount Rate – Growth Rate)
This is the foundation of the Gordon Growth Model used to value dividend-paying stocks in dividend investing strategies.
Present Value Calculator: Interactive Tool
💰 Present Value Calculator
Calculate what future money is worth in today’s dollars
FAQ: Present Value
There's no universally "good" present value—it depends entirely on context. A present value is favorable when it exceeds the cost of an investment or when it compares favorably to alternative opportunities. For example, if an investment opportunity has a present value of $50,000 but only costs $40,000, that's excellent because you're getting more value than you're paying. The key is comparing PV to what you must give up to obtain those future cash flows.
For quick mental estimates, use the Rule of 72 in reverse. Divide 72 by the interest rate to find how many years it takes for money to halve in present value. For example, at 8% discount rate, money 9 years away (72÷8) is worth roughly half today. For precise calculations, use the formula PV = FV / (1 + r)^n or financial calculators. Most smartphones have built-in calculator apps that can handle exponents, making PV calculations accessible anywhere.
Present Value (PV) is the current worth of future cash flows, while Net Present Value (NPV) subtracts the initial investment cost from the PV. Think of PV as "what future money is worth today" and NPV as "what future money is worth today minus what you have to pay for it." NPV directly tells you whether an investment creates or destroys value. A positive NPV means the investment is worth more than it costs; a negative NPV means you're overpaying.
In standard PV calculations with positive future cash flows and positive discount rates, present value itself cannot be negative—it will always be a positive number less than the future value. However, Net Present Value (NPV) can definitely be negative when the initial investment exceeds the present value of future returns. A negative NPV indicates an investment that destroys value and should typically be avoided.
Present value helps answer the critical retirement question: "How much do I need saved today to support my desired lifestyle in retirement?" By calculating the PV of your expected retirement expenses, you can determine your savings target. For instance, if you need $50,000 annually for 30 years in retirement, and you can earn 5% on investments, the present value is approximately $768,000—that's your retirement savings goal. Without PV calculations, you're essentially guessing at one of life's most important financial milestones.
Inflation reduces the purchasing power of future money, which should be reflected in your discount rate. You can handle inflation two ways: (1) Use nominal cash flows and nominal discount rates that include inflation, or (2) Use real (inflation-adjusted) cash flows and real discount rates. For example, if you expect 7% returns and 3% inflation, your real return is approximately 4%. Most personal finance calculations use nominal rates because they're easier to work with, but be aware that higher inflation environments require higher discount rates to maintain purchasing power.
Choose a discount rate that reflects your opportunity cost—what you could earn on alternative investments of similar risk. Here's a practical guide:
Low-risk decisions (guaranteed payments): Use current Treasury bond rates (4-5% in 2025)
Medium-risk decisions (stock market investments): Use historical stock market returns (7-10%)
High-risk decisions (startups, speculative investments): Use 12-20% or higher
Personal lending to friends/family: Consider your best alternative use for that money
The discount rate is partly subjective—it reflects your personal required return given the risk and your alternative opportunities.
Key Risks and Considerations
Risk 1: Discount Rate Selection Bias
Choosing too low a discount rate makes bad investments look good; choosing too high a rate makes good investments look bad. Always compare your discount rate to realistic alternative investments. If you're using 3% for a risky startup, you're fooling yourself. If you're using 15% for government bonds, you're being overly conservative.
Risk 2: Cash Flow Uncertainty
Present value calculations are only as good as your cash flow projections. Be conservative with estimates and consider running multiple scenarios (best case, worst case, most likely case) to understand the range of possible outcomes. This is especially important for understanding market volatility and how it affects long-term returns.
Risk 3: Changing Economic Conditions
Interest rates, inflation, and investment returns fluctuate over time, but most PV formulas assume constant rates. Build in a margin of safety by using slightly higher discount rates or lower cash flow estimates than your best guess. This buffer protects against unfavorable changes in economic conditions.
Risk 4: Ignoring Non-Financial Factors
Not everything valuable shows up in PV calculations. Job satisfaction, lifestyle preferences, family considerations, and personal goals matter too. Use PV as a tool for financial comparison, but not as the sole decision-maker. Sometimes the option with lower present value is still the right choice for non-financial reasons.
Real-World Success Story: Using PV to Make Smart Decisions
Let me share a story about Sarah, a 35-year-old marketing manager who used Present Value thinking to make a career-changing decision.
Sarah received two job offers:
Company A: $90,000 salary with $20,000 signing bonus
Company B: $95,000 salary with no signing bonus, but a guaranteed $10,000 annual bonus for the next 3 years
At first glance, Company A seemed better—$110,000 in year one versus $105,000 from Company B. But Sarah had learned about Present Value and decided to calculate the true value of each offer over 3 years.
She used an 8% discount rate (what she could earn investing in a diversified portfolio):
Company A total value:
- Year 1: $110,000 (base + signing bonus)
- Year 2: $90,000
- Year 3: $90,000
PV = $110,000 + $90,000/1.08 + $90,000/1.08² = $270,178
Company B total value:
- Year 1: $105,000 (base + bonus)
- Year 2: $105,000 (base + bonus)
- Year 3: $105,000 (base + bonus)
PV = $105,000 + $105,000/1.08 + $105,000/1.08² = $280,246
Company B was actually worth $10,068 more in present value terms! The consistently higher salary and guaranteed bonuses outweighed the attractive but one-time signing bonus.
Sarah chose Company B and never regretted it. Three years later, she'd built strong relationships there and was promoted, while several colleagues from Company A had left due to stagnant compensation after that initial signing bonus wore off.
This story illustrates how PV thinking helps you see past surface-level numbers to make decisions based on true economic value.
Conclusion: Making Present Value Work for You
Understanding Present Value transforms you from someone who makes financial decisions based on gut feeling into someone who makes them based on mathematical reality. The core insight—that money's value changes over time—is simple, but its applications touch nearly every financial decision you'll ever make.
Whether you're evaluating job offers, choosing between investment opportunities, planning for retirement, or deciding whether to buy or lease, Present Value gives you a framework for comparing options on equal footing. It's not about being perfectly precise (the future is inherently uncertain), but about being directionally correct and avoiding costly mistakes.
Your Action Steps
Here's how to start using Present Value in your financial life:
- Calculate your retirement number using the PV of annuity formula, how much do you need saved to generate your desired retirement income?
- Evaluate your next major purchase by comparing the present value of payment plans versus lump sum options
- Review your investment portfolio through a PV lens. Are you being adequately compensated for the time and risk involved?
- Use the interactive calculator above to practice with real numbers from your own financial decisions
- Learn about complementary concepts like passive income strategies that benefit from understanding the time value of money
- Teach these concepts to your children. An early understanding of PV is a gift that compounds over their lifetime
Remember, every dollar you invest today has the potential to become many dollars tomorrow. Present Value helps you understand exactly how much, and whether that's enough to justify the investment. It's the difference between hoping your financial decisions work out and knowing mathematically whether they make sense.
The wealthy don't have access to secret investment opportunities unavailable to everyone else. They simply understand concepts like Present Value and use them consistently to make better decisions. Now you have that same tool in your arsenal.
Start small, practice with the calculator, and gradually incorporate PV thinking into bigger decisions. Over time, it becomes second nature—a mental model that automatically activates whenever you encounter financial choices involving time.
Your future self will thank you for the smart financial moves you make today, armed with the power of Present Value.
Disclaimer
This article is for educational purposes only and does not constitute financial advice. Present Value calculations involve assumptions about future cash flows, discount rates, and economic conditions that may not materialize as expected. Always consult with a qualified financial advisor before making significant investments or financial decisions. Past performance does not guarantee future results. The examples provided are for illustrative purposes and may not reflect actual investment outcomes.
About the Author
Written by Max Fonji — With over a decade of experience in financial education and investment analysis, Max is your go-to source for clear, data-backed investing education. As the founder of TheRichGuyMath.com, Max has helped thousands of readers understand complex financial concepts through practical examples and actionable insights. His mission is to democratize financial knowledge and empower everyday investors to make informed decisions that build lasting wealth.







