When comparing savings accounts, credit cards, or loans, you’ll encounter two seemingly similar acronyms: APY and APR. Most people use these terms interchangeably, but this mistake can cost thousands of dollars over time. Understanding APY vs APR isn’t just financial jargon—it’s the math behind money that determines whether you’re maximizing earnings or minimizing costs.
The difference between these two rates reveals how compound interest works in your favor (or against you). APY accounts for compounding frequency, while APR does not. This single distinction changes everything about how your money grows or how much debt truly costs.
This guide breaks down the formulas, real-world applications, and strategic decisions that separate financially literate individuals from those who leave money on the table.
Key Takeaways
- APY (Annual Percentage Yield) includes compound interest effects and shows true earnings on savings accounts and investments
- APR (Annual Percentage Rate) represents the simple annual interest rate without compounding, used primarily for loans and credit cards
- APY is always higher than APR when comparing the same nominal rate with compounding periods
- For savings and investments, focus on APY—it reveals actual returns after compounding
- For loans and credit, focus on APR—but understand that actual costs may be higher due to fees and compounding
What Is APR? The Simple Interest Rate Explained
APR stands for Annual Percentage Rate. It represents the yearly cost of borrowing money or the simple annual return on an investment, expressed as a percentage.
The key characteristic of APR: it does not account for compound interest.
APR includes the base interest rate plus certain fees (like origination fees on loans), but it assumes interest is calculated only once per year. This makes APR a useful baseline comparison tool, but it doesn’t reflect the true cost or return when interest compounds more frequently.
The APR Formula
The basic APR calculation is straightforward:
APR = (Interest + Fees / Principal) × (365 / Loan Term in Days) × 100
For a simple annual interest rate without fees:
Interest = Principal × APR × Time
Where APR Appears
APR is the standard disclosure rate for:
- Credit cards (though they compound daily, making actual costs higher)
- Personal loans and installment debt
- Mortgages and home equity products
- Auto loans and vehicle financing
- Student loans and education debt
Financial institutions must disclose APR by law under the Truth in Lending Act, making it a standardized comparison metric. However, this legal requirement doesn’t mean APR tells the complete story.
APR Limitations
APR fails to capture:
- Compounding frequency (daily, monthly, quarterly)
- The exponential growth effect of reinvested interest
- True cost over time when payments reduce principal
When you understand compound vs simple interest, you recognize why APR alone is insufficient for financial decision-making.
What Is APY? The Compound Interest Reality
APY stands for Annual Percentage Yield. It represents the real rate of return earned on an investment or savings account over one year, accounting for the effect of compounding interest.
The defining feature of APY: it includes compound interest calculations.
APY shows what you actually earn when interest is reinvested and generates additional interest. This makes APY the accurate measure of growth for any account where interest compounds.
The APY Formula
The mathematical formula for APY is:
APY = (1 + r/n)^n – 1
Where:
- r = nominal interest rate (as a decimal)
- n = number of compounding periods per year
- ^n = raised to the power of n
Compounding Frequency Impact
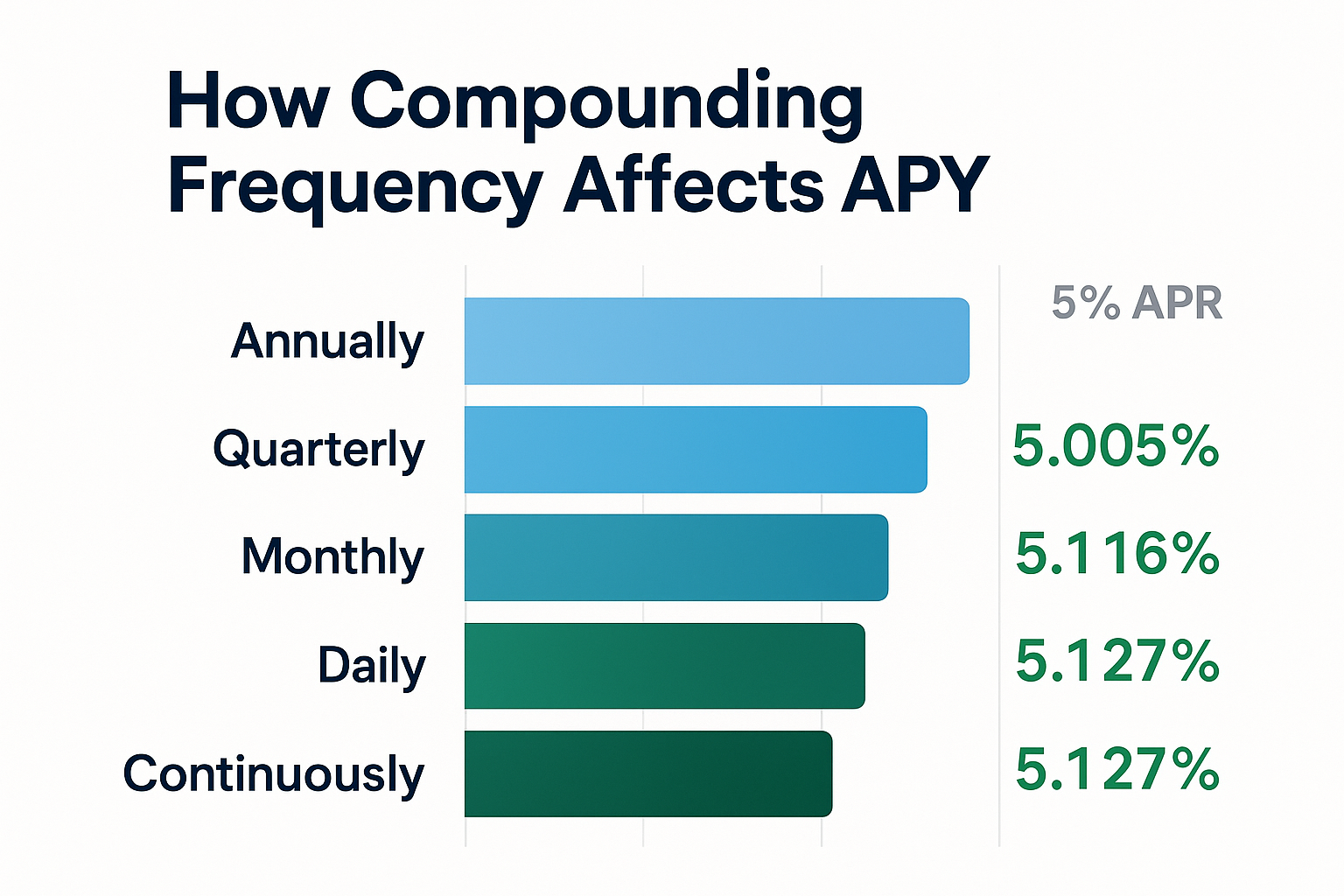
The more frequently interest compounds, the higher the APY relative to the stated interest rate:
| Compounding Frequency | Periods per Year (n) | APY on 5% Rate |
|---|---|---|
| Annually | 1 | 5.000% |
| Quarterly | 4 | 5.095% |
| Monthly | 12 | 5.116% |
| Daily | 365 | 5.127% |
| Continuously | ∞ | 5.127% |
This table demonstrates why APY matters. A 5% rate compounded daily yields 5.127%—an extra 0.127% that accumulates significantly over time.
Where APY Appears
APY is the standard disclosure for:
- High-yield savings accounts and money market accounts
- Certificates of deposit (CDs) and time deposits
- Interest-bearing checking accounts
- Bonds and fixed-income securities
- Dividend reinvestment plans (DRIPs)
Banks and financial institutions must disclose APY for deposit accounts under Regulation DD (Truth in Savings Act). This consumer protection ensures you can compare accounts accurately.
For those building emergency funds or exploring best compound interest accounts, APY is the only metric that matters.
APY vs APR: The Core Mathematical Difference
The fundamental distinction between APY and APR lies in one concept: compounding.
APR assumes simple interest—interest calculated only on the original principal. APY assumes compound interest—interest calculated on principal plus previously earned interest.
The Compounding Effect
Consider $10,000 at a 6% rate for one year:
APR Calculation (Simple Interest):
- Interest = $10,000 × 0.06 × 1 = $600
- Ending Balance = $10,600
- Effective Return = 6.000%
APY Calculation (Monthly Compounding):
- Monthly rate = 6% ÷ 12 = 0.5%
- Month 1: $10,000 × 1.005 = $10,050
- Month 2: $10,050 × 1.005 = $10,100.25
- Month 12: Final balance = $10,616.78
- Effective Return = 6.168%
The difference: $16.78 on a $10,000 investment. Over larger amounts and longer periods, this gap becomes substantial.
Why APY Is Always Higher
When comparing the same nominal rate:
APY ≥ APR
APY equals APR only when interest compounds annually (n=1). For all other compounding frequencies, APY exceeds APR because of the exponential growth from reinvested interest.
This mathematical reality explains why:
- Savings accounts advertise APY (a higher number attracts deposits)
- Credit cards emphasize APR (a lower number appears less expensive)
Understanding this asymmetry is essential for financial literacy and wealth building.
When to Focus on APY: Savings and Investment Accounts
Rule: When earning interest, maximize APY.
APY determines your actual returns on deposit accounts and fixed-income investments. The higher the APY and the more frequent the compounding, the faster your money grows.
High-Yield Savings Accounts
As of 2025, competitive high-yield savings accounts offer APYs between 4.00% and 5.50%. The difference between a 4.00% APY and 5.00% APY on $25,000 is $250 annually—enough to cover several months of streaming subscriptions or contribute to retirement.
Comparison example:
| Account Type | APY | $25,000 After 1 Year | $25,000 After 5 Years |
|---|---|---|---|
| Traditional Savings | 0.45% | $25,112.50 | $25,568.27 |
| High-Yield Savings | 5.00% | $26,250.00 | $31,907.04 |
| Difference | 4.55% | $1,137.50 | $6,338.77 |
This calculation assumes monthly compounding and no additional deposits. The five-year difference of $6,338.77 demonstrates why APY selection matters for emergency fund placement.
Certificates of Deposit (CDs)
CDs offer fixed APYs for specific terms (3 months to 5 years). Because your money is locked in, comparing APYs across different term lengths and institutions is critical.
CD ladder strategy:
- Divide savings into multiple CDs with staggered maturity dates
- Capture higher APYs on longer terms while maintaining liquidity
- Reinvest maturing CDs at prevailing rates
Money Market Accounts
Money market accounts combine checking-like access with savings-level APYs. They typically offer tiered APYs based on balance:
- $0-$9,999: 3.50% APY
- $10,000-$24,999: 4.00% APY
- $25,000+: 4.50% APY
This tiered structure incentivizes larger deposits and rewards savers who maintain higher balances.
Dividend Reinvestment and Compounding
When investing in dividend stocks or dividend ETFs, reinvesting dividends creates a compounding effect similar to APY. The effective yield increases as reinvested dividends purchase additional shares that generate their own dividends.
Example:
- Stock pays 4% annual dividend
- Dividends reinvested quarterly
- Effective annual yield (APY equivalent) = 4.06%
This compounding advantage is why long-term investors prioritize dividend growth stocks and dividend aristocrats that consistently increase payouts.
When to Focus on APR: Loans and Credit Products
Rule: When paying interest, minimize APR—but understand the full cost.
APR serves as the baseline comparison for borrowing costs, but the actual expense often exceeds the stated APR due to compounding and fee structures.
Credit Cards: Where APR Misleads
Credit card companies advertise APR, but they compound interest daily. This creates a significant gap between APR and the effective annual rate (EAR), which functions like APY for debt.
Example: 18% APR credit card
- Daily rate = 18% ÷ 365 = 0.0493%
- Effective Annual Rate = (1.000493)^365 – 1 = 19.72%
A $5,000 balance at 18% APR costs $986 in annual interest, not $900 as simple interest would suggest. This $86 difference compounds year after year if balances remain unpaid.
Strategy: Pay credit card balances in full monthly to avoid all interest charges. When carrying balances is unavoidable, prioritize cards with the lowest APR and consider debt consolidation options.
Personal Loans and Installment Debt
Personal loans typically use simple interest calculations based on APR, but origination fees (1% to 8% of the loan amount) increase the true cost.
Example: $10,000 personal loan
- APR: 9.99%
- Origination fee: 5% ($500)
- Net proceeds: $9,500
- True cost: Higher than 9.99% APR
Always calculate the effective rate, including all fees, when comparing loan offers.
Mortgage APR vs Interest Rate
Mortgages list both an interest rate and an APR. The APR includes:
- Base interest rate
- Origination fees
- Discount points
- Mortgage insurance premiums
- Other closing costs
Example:
- Interest rate: 6.50%
- APR: 6.73%
The 0.23% difference represents the annualized cost of fees spread over the loan term. A lower APR relative to the interest rate indicates fewer upfront costs.
For major purchases requiring financing, understanding the 20/4/10 rule for car buying helps maintain healthy debt ratios regardless of APR.
Auto Loans and Dealer Financing
Auto loans may advertise promotional 0% APR financing, but these offers typically require:
- Excellent credit scores (720+)
- Forfeiting manufacturer rebates
- Shorter loan terms (36-48 months)
Decision framework:
- Calculate total cost with 0% APR financing
- Calculate the total cost with the standard APR minus available rebates
- Choose the option with the lower total payment
Dealer financing often includes hidden fees that increase the effective APR beyond the advertised rate.
The Conversion Formula: APR to APY and Back
Understanding how to convert between APR and APY provides clarity when comparing different financial products.
Converting APR to APY (Effective Annual Rate)
Formula: APY = (1 + APR/n)^n – 1
Where n = compounding periods per year
Example: 12% APR with monthly compounding
- APY = (1 + 0.12/12)^12 – 1
- APY = (1.01)^12 – 1
- APY = 1.1268 – 1
- APY = 0.1268 or 12.68%
Converting APY to APR
Formula: APR = n × [(1 + APY)^(1/n) – 1]
Example: 12.68% APY with monthly compounding
- APR = 12 × [(1.1268)^(1/12) – 1]
- APR = 12 × [1.01 – 1]
- APR = 12 × 0.01
- APR = 0.12 or 12%
Quick Reference Conversion Table
| APR | Daily Compound APY | Monthly Compound APY | Quarterly Compound APY |
|---|---|---|---|
| 3% | 3.045% | 3.042% | 3.034% |
| 5% | 5.127% | 5.116% | 5.095% |
| 7% | 7.250% | 7.229% | 7.186% |
| 10% | 10.516% | 10.471% | 10.381% |
| 15% | 16.180% | 16.075% | 15.865% |
| 20% | 22.134% | 21.939% | 21.551% |
This table reveals how compounding frequency amplifies the difference between APR and APY at higher rates—a critical insight for both debt management and investment selection.
Real-World Scenarios: APY vs APR in Action
Scenario 1: Choosing a Savings Account
Situation: You have $15,000 for an emergency fund and are comparing two accounts:
Account A:
- Advertised rate: 4.75% APR
- Compounding: Annually
- Actual APY: 4.75%
Account B:
- Advertised rate: 4.70% APR
- Compounding: Daily
- Actual APY: 4.81%
Analysis:
Despite Account A’s higher APR, Account B delivers superior returns:
- Account A after 1 year: $15,712.50
- Account B after 1 year: $15,721.50
- Difference: $9.00
Over 10 years with monthly $200 deposits:
- Account A: $42,847.23
- Account B: $43,094.67
- Difference: $247.44
Decision: Choose Account B. The higher APY from daily compounding outperforms the higher APR with annual compounding.
This principle applies when selecting among best compound interest accounts for long-term wealth building.
Scenario 2: Credit Card Balance Transfer
Situation: You carry an $8,000 credit card balance and receive two balance transfer offers:
Offer A:
- 0% APR for 18 months
- 3% balance transfer fee ($240)
- 19.99% APR after promotional period
Offer B:
- 5.99% APR for 24 months
- 0% balance transfer fee
- 18.99% APR after promotional period
Analysis:
Offer A total cost (paying $500/month):
- Transfer fee: $240
- Interest during promo: $0
- Balance paid in 16 months
- Total cost: $240
Offer B total cost (paying $500/month):
- Transfer fee: $0
- Interest over 16 months: ~$387
- Balance paid in 16 months
- Total cost: $387
Decision: Choose Offer A. The upfront fee is less than the accumulated interest from Offer B’s 5.99% APR, even with daily compounding.
Scenario 3: Investment Account Comparison
Situation: Comparing a high-yield savings account to a short-term bond fund:
Option A: High-Yield Savings
- 5.00% APY
- FDIC insured
- Daily compounding
- No fees
Option B: Short-Term Bond Fund
- 5.50% stated yield
- Not FDIC insured
- 0.25% annual expense ratio
- Market value fluctuation risk
Analysis:
- Savings account guaranteed return: 5.00%
- Bond fund net return: 5.50% – 0.25% = 5.25% (before potential losses)
For emergency fund purposes, the savings account’s guaranteed APY with FDIC protection outweighs the bond fund’s slightly higher potential return with added risk.
For investment portfolios beyond emergency reserves, diversification strategies balance risk and return across multiple asset classes.
Common Misconceptions About APY and APR
Misconception 1: “APR and APY are basically the same thing.”
Reality: APR excludes compounding effects; APY includes them. This difference can represent hundreds or thousands of dollars over time.
The math behind money requires precision. Treating these rates as interchangeable leads to suboptimal financial decisions.
Misconception 2: “Higher APR always means higher cost”
Reality: APR must be evaluated alongside:
- Compounding frequency
- Fee structures
- Loan term length
- Payment schedules
A 6% APR loan with quarterly compounding costs more than a 6% APR loan with annual compounding. The effective annual rate (EAR) determines true cost.
Misconception 3: “APY only matters for large account balances”
Reality: APY matters at every balance level because of compound growth over time.
Example: $1,000 initial deposit with $100 monthly contributions
| APY | Balance After 5 Years | Balance After 20 Years |
|---|---|---|
| 3.00% | $7,462 | $33,080 |
| 5.00% | $7,989 | $41,103 |
| Difference | $527 | $8,023 |
Even modest balances benefit significantly from higher APY over extended periods. This demonstrates why compound growth is the foundation of wealth building.
Misconception 4: “0% APR means free money”
Reality: 0% APR promotional offers often include:
- Balance transfer fees (3-5%)
- Origination fees (1-8%)
- Deferred interest charges if not paid in full
- Higher rates after promotional period
Calculate the total cost, including all fees, to determine if 0% APR offers truly save money compared to alternatives.
Misconception 5: “APY is guaranteed forever”
Reality: APY on savings accounts and money market accounts is variable and can change:
- Daily (at the institution’s discretion)
- In response to Federal Reserve rate changes
- Based on account balance tiers
Only CDs and fixed-rate bonds lock in APY for specified terms. Variable-rate accounts require ongoing monitoring to ensure competitive returns.
How Federal Reserve Policy Affects APY and APR
The Federal Reserve’s federal funds rate directly influences both APY and APR across the financial system.
The Interest Rate Transmission Mechanism
Federal Reserve raises rates →
- Banks’ borrowing costs increase
- Banks raise APR on loans and credit cards
- Banks raise APY on deposit accounts (usually with a lag)
Federal Reserve lowers rates →
- Banks’ borrowing costs decrease
- Banks lower the APR on loans and credit cards
- Banks lower APY on deposit accounts (usually immediately)
The APY-APR Spread
Financial institutions profit from the spread between:
- APR charged on loans (revenue)
- APY paid on deposits (expense)
This net interest margin typically ranges from 2.5% to 4.0% and represents the bank’s core profitability.
Example in 2025:
- Average credit card APR: 20.74%
- Average savings account APY: 0.45%
- Spread: 20.29 percentage points
High-yield savings accounts narrow this spread by offering competitive APYs (4.00-5.50%), which is why they’re typically offered by online banks with lower overhead costs.
Rate Environment Strategy
Rising rate environment (2022-2023):
- Lock in fixed-rate loans before rates increase further
- Keep savings in variable-rate accounts to capture rising APYs
- Consider short-term CDs to maintain flexibility
Falling rate environment (2024-2025):
- Refinance variable-rate debt to fixed rates
- Lock in higher APYs with longer-term CDs before rates drop
- Accelerate debt payoff while rates remain elevated
Understanding monetary policy helps optimize both borrowing costs and savings returns. This macroeconomic awareness complements investing fundamentals for comprehensive financial planning.
Calculating Your True Return or Cost: The EAR Formula
The Effective Annual Rate (EAR) provides the most accurate measure of true return or cost by accounting for compounding frequency.
The EAR Formula
EAR = (1 + i/n)^n – 1
Where:
- i = stated interest rate (APR for loans, nominal rate for savings)
- n = number of compounding periods per year
Why EAR Matters More Than APR or APY
EAR standardizes all financial products to a comparable annual rate, regardless of:
- Compounding frequency differences
- Payment schedules
- Fee structures (when included in calculation)
Example comparison:
| Product | Stated Rate | Compounding | EAR |
|---|---|---|---|
| Savings Account | 5.00% APY | Daily | 5.127% |
| CD | 5.10% APY | Monthly | 5.221% |
| Bond | 5.25% yield | Semi-annual | 5.316% |
| Credit Card | 18.00% APR | Daily | 19.72% |
The EAR column enables direct comparison across different product types and compounding schedules.
Calculating EAR with Fees
To include fees in the EAR calculation:
EAR = [(Total Interest + Fees) / Net Principal] × (365 / Days)
Example: $10,000 loan
- APR: 8.00%
- Origination fee: $300
- Term: 1 year
- Interest: $800
- Total cost: $1,100
- Net proceeds: $9,700
EAR = ($1,100 / $9,700) × (365 / 365) = 11.34%
The true cost (11.34%) significantly exceeds the stated APR (8.00%), revealing the importance of fee analysis in borrowing decisions.
Strategic Decision Framework: APY vs APR
Use this decision framework to optimize financial choices:
For Savings and Investment Accounts
Priority ranking:
- Maximize APY (higher is always better)
- Verify compounding frequency (daily > monthly > quarterly > annual)
- Confirm FDIC/NCUA insurance (for deposit accounts)
- Evaluate accessibility (withdrawal restrictions, minimum balances)
- Consider tax implications (interest is taxable income)
Action steps:
- Compare APYs across at least 3-5 institutions
- Calculate actual dollar returns on your expected balance
- Review account terms for rate guarantees vs. variable rates
- Set calendar reminders to review rates quarterly
For Loans and Credit Products
Priority ranking:
- Minimize APR (lower is always better)
- Calculate EAR, including all fees (true cost comparison)
- Understand compounding frequency (affects total interest paid)
- Evaluate total payment amount (not just monthly payment)
- Consider prepayment flexibility (ability to pay off early)
Action steps:
- Obtain written quotes from at least 3 lenders
- Calculate total interest paid over the full loan term
- Negotiate fees and rates (especially origination fees)
- Review payment schedule and amortization table
For Complex Financial Decisions
When comparing products with different structures:
Step 1: Convert all rates to EAR for standardized comparison
Step 2: Calculate total dollar cost or return over the relevant time period
Step 3: Adjust for risk differences (FDIC insurance, credit risk, market risk)
Step 4: Consider liquidity needs and access requirements
Step 5: Evaluate tax treatment and after-tax returns
This systematic approach ensures data-driven decisions based on evidence rather than marketing claims or surface-level rate comparisons.
For those building comprehensive financial plans, this framework integrates with budgeting strategies and wealth building principles.
The Tax Implications of APY and APR
Both APY and APR have tax consequences that affect net returns and costs.
Interest Income from APY (Taxable)
Interest earned from savings accounts, CDs, and money market accounts is taxable as ordinary income.
Tax treatment:
- Reported on Form 1099-INT (if over $10 annually)
- Taxed at your marginal income tax rate
- No special capital gains treatment
Example: $10,000 at 5.00% APY
- Annual interest: $500
- Tax at 24% marginal rate: $120
- After-tax return: $380 (3.80% after-tax APY)
After-tax APY formula:
After-tax APY = APY × (1 – Marginal Tax Rate)
| Marginal Tax Rate | 5.00% APY After-Tax | 4.00% APY After-Tax |
|---|---|---|
| 12% | 4.40% | 3.52% |
| 22% | 3.90% | 3.12% |
| 24% | 3.80% | 3.04% |
| 32% | 3.40% | 2.72% |
| 35% | 3.25% | 2.60% |
This tax drag reduces effective returns, making tax-advantaged accounts (Roth IRAs, 401(k)s) more attractive for long-term savings despite potentially lower nominal APYs.
Interest Expense from APR (Sometimes Deductible)
Interest paid on loans has varying tax treatment:
Deductible interest:
- Mortgage interest (up to $750,000 loan limit)
- Student loan interest (up to $2,500, income limits apply)
- Business loan interest
- Investment interest (limited to investment income)
Non-deductible interest:
- Credit card interest
- Personal loan interest
- Auto loan interest (unless for business use)
Example: Mortgage at 6.50% APR
- Annual interest on $300,000: $19,500
- Tax deduction at 24% rate: $4,680
- After-tax cost: $14,820 (4.94% after-tax APR)
After-tax APR formula:
After-tax APR = APR × (1 – Marginal Tax Rate)
This tax benefit makes mortgage debt more affordable than the stated APR suggests, but only for itemizers who exceed the standard deduction.
Strategic Tax Planning
Maximize tax efficiency:
- Use tax-advantaged accounts for the highest-APY investments
- Keep taxable accounts for tax-efficient investments (index funds, municipal bonds)
- Prioritize paying off non-deductible debt (credit cards) before deductible debt (mortgages)
- Consider municipal bonds for high-income earners (tax-free interest)
Understanding these tax implications ensures accurate comparison of after-tax returns and costs—the only metrics that matter for actual wealth accumulation.
Tools and Resources for Comparing APY vs APR
Online Calculators
APY Calculator:
Input: Principal, interest rate, compounding frequency, time period
Output: Total interest earned, final balance, effective APY
APR to APY Converter:
Input: APR, compounding frequency
Output: Equivalent APY/EAR
Loan Comparison Calculator:
Input: Loan amount, APR, fees, term
Output: Total interest paid, monthly payment, EAR
Savings Growth Calculator:
Input: Initial deposit, monthly contribution, APY, time period
Output: Future value, total interest earned, contribution breakdown
Comparison Websites
For savings accounts:
- Bankrate.com (comprehensive rate tables)
- DepositAccounts.com (detailed APY comparisons)
- NerdWallet.com (editorial reviews and rate tracking)
For loans and credit:
- Credible.com (personal loan comparisons)
- LendingTree.com (multiple lender quotes)
- CardRatings.com (credit card APR comparisons)
Spreadsheet Templates
Create custom comparison spreadsheets with:
- APY/APR conversion formulas
- Side-by-side product comparisons
- Total cost/return calculations over time
- After-tax return adjustments
- Scenario analysis (different deposit amounts, time periods)
Sample Excel formulas:
APY from APR:=POWER(1+(APR/n),n)-1
Monthly payment:=PMT(APR/12, months, -principal)
Future value with regular deposits:=FV(APY/12, months, -monthly_deposit, -initial_deposit)
Professional Resources
For complex financial decisions:
- Certified Financial Planner (CFP) consultation
- Fee-only financial advisor analysis
- CPA for tax-optimization strategies
- Mortgage broker for loan comparisons
Professional guidance provides personalized analysis beyond generic calculators, especially for large financial commitments
APY vs APR Calculator
Compare the true cost of borrowing or real return on savings
| Compounding Frequency | APY | Final Balance | Difference |
|---|
Key Insight: The difference between APR and APY grows with more frequent compounding. Daily compounding maximizes returns on savings but increases costs on debt. Always compare APY for savings accounts and calculate the effective annual rate (EAR) for loans.
Conclusion: Making APY and APR Work for Your Financial Goals
The distinction between APY vs APR represents more than financial terminology—it’s the mathematical foundation of wealth building and debt management.
Core principles to remember:
For earning money, APY reveals true returns through compound interest. Maximize APY on savings accounts, CDs, and investment accounts. Even small APY differences compound into substantial wealth over time.
For borrowing money: APR provides the baseline cost, but calculate the effective annual rate (EAR), including fees and compounding, to understand the true expense. Minimize APR and pay off high-rate debt aggressively.
For financial decisions: Convert all rates to comparable metrics (EAR), calculate dollar amounts over relevant time periods, and adjust for tax implications. Data-driven decisions based on mathematical reality outperform emotional reactions to marketing claims.
The math behind money doesn’t lie. A 5.00% APY with daily compounding delivers 5.127% actual returns. An 18% APR credit card costs 19.72% when compounded daily. These numbers determine whether you build wealth or subsidize financial institutions.
Actionable next steps:
- Audit your current accounts: List all savings accounts, loans, and credit cards with their APY or APR rates
- Calculate true returns and costs: Convert rates to EAR and determine annual dollar amounts
- Compare against market rates: Research competitive APYs for savings and APRs for refinancing opportunities
- Optimize your highest-impact accounts first: Focus on your largest balances where rate differences create maximum dollar impact
- Set quarterly review reminders: Monitor rate changes and market conditions every 3 months
- Educate yourself continuously: Understanding compound interest, time value of money, and interest rate mathematics builds lasting financial literacy
The difference between financial success and struggle often comes down to understanding these fundamental concepts and applying them consistently. APY and APR aren’t just acronyms—they’re the quantitative tools that transform financial knowledge into measurable wealth building.
Master the math behind money, and you master your financial future.
References
[1] Federal Reserve Board. (2025). “Truth in Savings (Regulation DD).” Board of Governors of the Federal Reserve System.
[2] Consumer Financial Protection Bureau. (2025). “What is the difference between a mortgage interest rate and an APR?” CFPB.
[3] Securities and Exchange Commission. (2025). “Compound Interest Calculator.” SEC Office of Investor Education.
[4] Federal Deposit Insurance Corporation. (2025). “Savings Account Rates: National Rate and Rate Cap Information.” FDIC.
[5] Board of Governors of the Federal Reserve System. (2025). “Federal Funds Rate Historical Data.” Federal Reserve Economic Data
[6] Internal Revenue Service. (2025). “Topic No. 403 Interest Received.” IRS Tax Information.
[7] CFA Institute. (2025). “Time Value of Money and Interest Rate Calculations.” CFA Program Curriculum.
Author Bio
Max Fonji is the founder of The Rich Guy Math, a data-driven financial education platform that explains the mathematical principles behind wealth building, investing, and risk management. With expertise in financial analysis and valuation, Max translates complex financial concepts into actionable insights for investors at all levels. His evidence-based approach combines quantitative analysis with practical application, helping readers understand not just what to do with money, but why the math works.
Educational Disclaimer
This article is provided for educational and informational purposes only and does not constitute financial, investment, tax, or legal advice. The information presented represents general principles and mathematical concepts related to APY and APR calculations. Individual financial situations vary significantly based on personal circumstances, risk tolerance, tax status, and financial goals.
Interest rates, APY, and APR figures cited are examples and may not reflect current market conditions. Actual rates vary by institution, creditworthiness, account type, and economic conditions. Always verify current rates and terms directly with financial institutions before making decisions.
Consult with qualified financial advisors, certified public accountants, and legal professionals for personalized guidance tailored to your specific situation. Past performance and mathematical examples do not guarantee future results. All investment and borrowing decisions carry risk, including potential loss of principal.
The Rich Guy Math and its authors are not registered investment advisors, financial planners, or licensed tax professionals. This content is designed to enhance financial literacy and understanding of fundamental concepts, not to provide specific recommendations for individual financial products or strategies
Frequently Asked Questions
Is APY or APR better for savings accounts?
APY is the correct metric for savings accounts. APY includes the effect of compound interest, showing your actual earnings. A savings account with 5.00% APY earns more than one with 5.00% APR (which would only be 5.00% APY if compounded annually). Always compare savings accounts using APY, and choose accounts with daily or monthly compounding for maximum growth.
Can APR be higher than APY?
No, APR cannot be higher than APY for the same nominal interest rate. When interest compounds more than once per year, APY will always exceed APR because compound interest generates additional returns. APY equals APR only when compounding occurs annually (once per year). The more frequent the compounding, the greater the difference between APR and APY.
Why do credit cards show APR instead of APY?
Credit cards show APR because it appears lower than the effective annual rate (EAR). However, credit cards compound interest daily, which means the true cost exceeds the stated APR. A 18% APR credit card with daily compounding has an effective annual rate of 19.72%. This disclosure practice is required by law but can mislead consumers about actual borrowing costs.
How often should I compare APY rates on my savings account?
Review savings account APY rates quarterly. Banks can change variable APY rates at any time, and competitive rates fluctuate with Federal Reserve policy changes. Set a calendar reminder every 3 months to compare your current APY against top-performing accounts. If your APY has dropped significantly below market rates (0.50% or more), consider switching to a higher-yield account.
Does a higher APY always mean a better savings account?
Not always—evaluate the complete account structure. While APY is the primary factor, also consider: FDIC insurance coverage, minimum balance requirements, monthly fees, withdrawal restrictions, customer service quality, and digital banking features. A slightly lower APY (within 0.10-0.25%) may be acceptable if other features better match your needs. However, APY differences exceeding 0.50% generally outweigh other factors.
How do I calculate the real difference between two APY rates?
Use this formula: Future Value = Principal × (1 + APY)^Years
Example comparing 4.00% APY vs. 5.00% APY on $20,000 over 10 years:
- 4.00% APY: $20,000 × (1.04)^10 = $29,604.89
- 5.00% APY: $20,000 × (1.05)^10 = $32,577.89
Difference: $2,973.00 — this calculation shows the actual dollar impact of APY differences over your intended savings period.
Should I prioritize paying off high APR debt or building savings with high APY?
Prioritize high APR debt payoff first. The interest cost on debt (15–25% APR typical for credit cards) far exceeds interest earned on savings (4–5% APY typical for high-yield accounts). The guaranteed “return” from eliminating 20% APR debt is 20%—far better than any savings account. Exception: Maintain a small emergency fund ($1,000–$2,000) before aggressive debt payoff to avoid new debt from unexpected expenses.
What’s the relationship between APY and compound interest?
APY measures the effect of compound interest over one year. Compound interest means earning interest on previously earned interest. APY captures this exponential growth by showing the total percentage increase, including all compounding periods. The formula APY = (1 + r/n)^n - 1 mathematically expresses how compounding frequency (n) amplifies returns beyond the nominal rate (r). Understanding compound vs simple interest reveals why APY matters for long-term wealth building.







